6. Sınıf Geometrik Cisimler Konu Anlatımı

6. Sınıf Geometrik Cisimler Konu Anlatımı, 6. Sınıf Geometrik Cisimler , Geometrik Cisimler Konu Anlatımı, 6. Sınıf Matematik , 6. Sınıf Matematik Konu Anlatımı, Geometrik Cisimler

Geometrik Cisimler

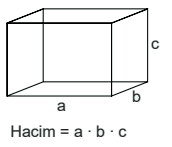
Dikdörtgenler Prizmasının Hacmi

Dikdörtgenler prizmasının hacmi, ayrıt uzunluklarının çarpımına eşittir.

Örnek

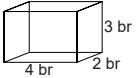
Yukarıdaki dikdörtgenler prizmasının hacmini bulalım.

Hacim = 4 . 2 . 3 = 24 br³

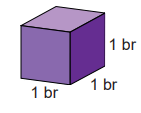
Bir ayrıtının uzunluğu 1 br olan küpe birimküp denir.

Örnek

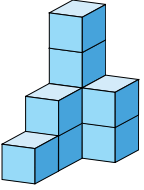
Yukarıdaki şekildeki  şekli prizmaya tamamlamak için kaç tane birimküp gerekir?

Hacim = 4 . 2. 3 = 24 birimküp

4 + 2 + 3 = 13

24 – 13 = 11 birimküp gereklidir.

Prizmaların hacmi prizmayı oluşturan birim küplerin sayısına eşittir.

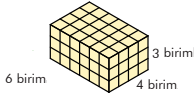
Hacim = 6 birim × 3 birim × 4 birim

Hacim = 72 birimküptür.
Prizma 72 adet birimküpten oluşmuştur.
Birimküp, (br³) olarak gösterilir.

Kare Prizmanın Hacmi

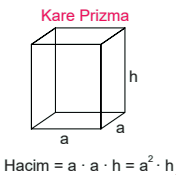
Kare prizmanın hacmi, taban alanı ve yüksekliğin çarpımı ile bulunur. Taban alanı ise eş olan taban ayrıt uzunluklarının çarpımıdır.

Örnek

Kare prizma şeklindeki bir hediye kutusunun taban ayrıt uzunluğu 5 birim ve yüksekliği 7 birim olduğuna göre hediye kutusunun hacminin kaç birimküp olduğunu bulunuz.

Hacim = 5 . 5 . 7 = 175 birimküp

Küpün Hacmi

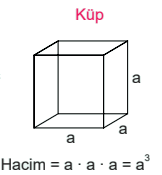
Küpün hacmi, eş olan taban ayrıt uzunlukları ve yüksekliğin çarpımıyla bulunur. Taban ayrıt uzunlukları ve yükseklik eşittir.

Örnek

Yukarıdaki şekilde birimküplerden oluşan zeka oyununun hacminin kaç br³ olduğunu bulunuz.

Hacim = 4. 4. 4 = 64 br³

6. Sınıf Matematik Konuları için tıklayınız.