6. Sınıf Alan Ölçme Konu Anlatımı

6. Sınıf Alan Ölçme Konu Anlatımı, 6. Sınıf Alan Ölçme , Alan Ölçme Konu Anlatımı, 6. Sınıf Matematik , 6. Sınıf Matematik Konu Anlatımı, Alan Ölçme
Alan Ölçme
Üçgenin Alanı
Üçgenin bir köşesinden karşı kenarına çizilen dikmeye yükseklik denir ve yükseklik h harfiyle gösterilir. Üçgenin üç farklı yüksekliği vardır. Yüksekliğin çizildiği kenara ise taban adı verilir.
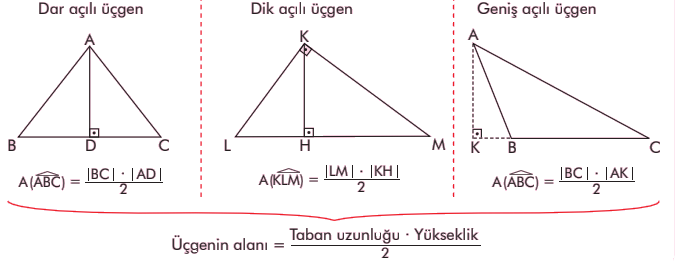
Örnek-1
Taban uzunluğu 15 m ve bu tabana ait yüksekliği 6 m olan üçgenin alanı kaç metrekaredir?
15 . 6 = 90 / 2 = 45 metrekaredir.
Örnek-2
Aşağıdaki ABC geniş açılı üçgeninin alanı 20 santimetrekaredir. |AB| = 4 cm ise [AB] kenarına ait yükseklik kaç santimetredir?
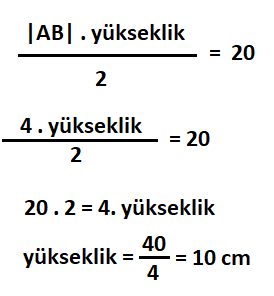
Örnek-3
Aşağıda verilen KLM dik üçgeninde |KL| = 10 cm ve |KM| = 5 cm ise KLM üçgen alanı kaç santimetre karedir?
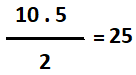
Paralelkenarın Yüksekliği ve Alanı
Karşılıklı kenar uzunlukları paralel ve eşit uzunlukta, karşılıklı açıları eşit olan dörtgenlere paralelkenar denir.
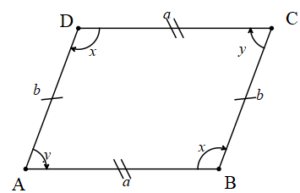
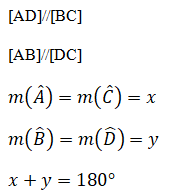
Paralelkenarın bir köşesinden karşı kenarına çizilen dikmeye yükseklik denir. Yükseklik h harfi ile gösterilir. Yüksekliğin çizildiği kenara taban denir. Paralelkenarın iki farklı yüksekliği vardır.
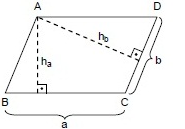
Paralelkenarın alanı taban uzunluğu ile yüksekliğin çarpımına eşittir.
![]()
Örnek-1
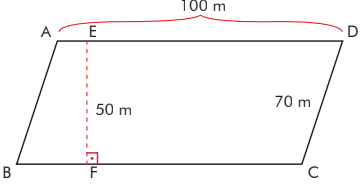
Şekilde verilenlere göre paralel kenarın alanını bulunuz.
A(ABCD) = taban . yükseklik
A (ABCD)= 100 . 50 =5000 metrekaredir.
Örnek-2

Yukarıdaki paralelkenarın alanı 50 santimetrekare ise [DC] kenarına ait yükseklik kaç santimetredir?
A(ABCD) = taban . yükseklik
50 = 5 . yükseklik
50 / 5 = yükseklik
yükseklik = 10 santimetrekaredir.
Örnek-3
Aşağıdaki paralelkenarın alanı kaç metrekaredir?
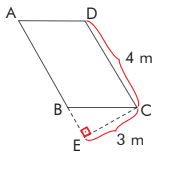
A(ABCD) = taban . yükseklik
A(ABCD) = 4. 3 = 12 metrekaredir.
Alan Ölçü Birimleri
Alan ölçerken temel ölçü birimimiz metrekare (m2) ‘dir.
Örnek
Odamızın büyüklüğünü, sınıfımızın büyüklüğünü ifade ederken metrekare kullanırız.
Daha küçük alanları ifade ederken desimetrekare (dm2), santimetrekare (cm2) ve milimetrekare (mm2) birimlerini kullanabiliriz.
Örnek
Çalışma masamızın alanını desimetrekare, defter ve kitaplarımızın alanını santimetrekare, silgi, kalemtıraş gibi daha küçük eşyalarımızın alanını ifade ederken milimetrekare kullanırız.
Daha büyük alanları ifade ederken dekametrekare (dam2), hektometrekare (hm2) ve kilometrekare (km2) birimlerini kullanabiliriz.
Örnek
Futbol sahaların alanını ve bahçemizin alanını dekametrekare ile, mahallemizin alanını hektometrekare, il ilçe ve ülke gibi daha büyük alanları ifade ederken kilometrekare kullanırız.
Alan Ölçü Birimlerini Birbirine Dönüştürme
Büyük birimler küçük birimlere çevriliyorsa verilen sayı inilen her basamak için 100 ile çarpılır. Küçük birimler büyük birimlere çevriliyorsa verilen sayı inilen her basamak için 100 ile bölünür.

Örnek-1

Örnek-2

Örnek-3
3 m2 = 300 cm2
100 000 mm2= 100 cm2
72 km2 = 720 m2
45 m2 = 450 cm2
Örnek-4
Selim amcanın dikdörtgen şeklindeki çiftliğinin uzun kenarı 0,025 kilometre, kısa kenarı ise 0,020 kilometredir. Çiftliğin içerisinde hayvanların barındıkları yer 200 metrekare ve sebze ekili alan 150 metrekaredir. Kalan alanı ağaç dikerek değerlendirmek isteyen Selim amcanın kaç metrekarelik alana ağaç dikeceğini bulalım.
0,025 km = 0,025 · 1000 = 25 m
0,020 km = 0,020 · 1000 = 20 m
Dikdörtgenin alanı: 25 m · 20 m = 500 m2
Hayvanların barındıkları ve sebze ekili alanların toplamı:
200 m2 + 150 m2 = 350 m2
Ağaç dikilecek alan: 500 m2– 350 m2 = 150 m2
Arazi Ölçü Birimleri
Bahçe, tarla, arsa gibi yerlerin alanını ölçmek için arazi ölçme birimleri olan ar, dekar (dönüm) ve hektar kullanılır. Arazi ölçmede temel birim olarak ar kullanılır. Alan ölçü birimleri ile arazi ölçü birimleri arasında ilişki kurulabilir.
1 hektar (ha) = 10 dekar (daa) = 100 ar (a)
1 dekar (daa) = 1 dönüm = 1000 m2
Örnek-1
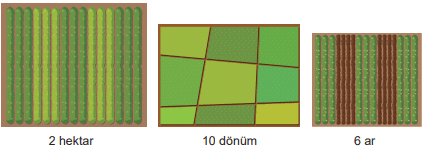
Bir baba, 3 oğlu ve 1 kızına 6 ar, 10 dönüm ve 2 hektarlık araziyi, her birinin her arazide payı olacak şekilde paylaştırıyor.
Baba, dört çocuğuna eşit paylaşım yaptığına göre kızına kaç metrekare arazi payı düşmüştür?
2 hektar = 20 dekar = 20000 m2
10 dönüm = 10000 m2
6 ar = 600 m2
20000 m2 + 10000 m2 + 600 m2 = 30600 m2
30600 m2 : 4 = 7650 m2
Örnek-2
Çatalhöyük Neolitik Kenti hakkında araştırma yapmak isteyen arkeoloji öğrencileri 14 hektarlık alanı bir haftada
gezecektir. Buna göre öğrencilerin bir günde kaç dekarlık alanı gezeceğini bulalım.
1 ha = 10 daa = 100 a
14 ha = 14 · 10 = 140 daa
Birlikte Öğrenelim
Bir haftada 140 daa’lık alan gezen öğrenciler bir günde 140 ÷ 7 = 20 daa’lık alan gezer.






