Merkezi Yayılım (Dağılım) Ölçüleri Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Merkezi Yayılım (Dağılım) Ölçüleri konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Merkezi Yayılım (Dağılım) Ölçüleri
Açıklık (Aralık – Ranj)
Sonlu bir veri grubunda en büyük terimden en küçük terimi çıkartarak bulunan değerdir.
R = En Büyük Değer – En Küçük Değer
Örnek
7, 3, 4, 9, 2, 7, 5 veri grubunun açıklığını (Ranjını) bulunuz.
Çözüm: R = 9 – 2 = 7 dir.
Örnek
26, 16, 16, 33, 55, 109 sayılarından en büyük olan 109 en küçük olan 16 dır.
Buna göre verilen sayıların açıklığı, 109 – 16 = 93 tür.
Çeyrekler Açıklığı
Bir veri grubundaki terimler küçükten büyüğe doğru sıralandığında ilk terime en küçük, son terime en büyük, bunların ortasındaki terime de ortanca denir.
Ortancadan küçük olan terimlerin ortancasına alt çeyrek (Q1) denir.
Ortancadan büyük olan terimlerin ortancasına üst çeyrek(Q3) denir.
Bir başka ifade ile veri kümesinin ilk % 50 lik kısmının ortancasına Q1 , sonraki % 50 lik kısmının ortancasına da Q3 denir.
Örnek
2, 3 , 6, 9, 5, 10, 4, 2, 9, 8, 5 verilerinin oluşturduğu grubun çeyrekler açıklığını bulalım.
Verileri küçükten büyüğe sıraya koyalım.
2, 2, 3, 4, 5, 5, 6, 8, 9, 9, 10
Ortanca terim, alt uçtan ve üst uçtan eşit uzaklıkta olan terimdir. Veya Q=1/2(n+1) inci terimdir. 6. terim yapar
2, 2, 3, 4, 5, 5, 6, 8, 9, 9, 10
ortanca terim( Medyan)
Alt çeyrek: 2, 2, 3, 4, 5 verilerinin ortadaki elemanı olan 3 tür.
Üst çeyrek: 6, 8, 9, 9, 10 verilerinin ortadaki elemanı olan 9 dur
Çeyrekler açıklığı: 9 – 3 = 6 bulunur.
Standart Sapma
Sonlu bir nicel veri dizisinde her bir elemanın aritmetik ortalama ile olan farkının karelerinin toplamının veri adedinin bir eksiğine bölümünün kare köküdür.
Düşük standart sapma değeri, bir araya toplanmış ve ortalamaya daha yakın verilerin çok olduğunun ölçüsüdür. n tane verinin aritmetik ortalaması x olmak üzere, bu veri grubunun standart sapması (s);
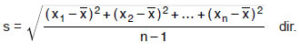
Örnek
1, 7, 8, 9, 10, 13, 50 veri grubunun standart sapmasını bulalım.
Ortalama
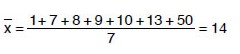
Standart Sapma
![]()






