8. Sınıf Doğrusal Denklemler Konu Anlatımı

Bu yazımızda sizlere LGS Matematik konusu olan aynı zamanda 8. sınıf konuları arasında yer alan Doğrusal Denklemler hakkında bilgilendireceğiz. Aşağıda sizlere başlıklar halinde konularımızı anlattık. Üzerine tıklayarak ulaşabilirsiniz.
Doğrusal Denklemler
- Bir Bilinmeyenli Denklemler
- Koordinat Sistemi
- Doğrusal İlişki ve Doğrusal Denklemler
- Doğrusal Denklemlerin Grafikleri
- Eğim
x ve y iki değişken olmak üzere ax + by + c = 0 şeklindeki denklemlere doğrusal denklem denir. Bu ifadedeki c sayısına sabit sayı, a, b ve c sayılarına kat sayı adı verilir. a ve b kat sayıları aynı anda 0 (sıfır) değerini alamaz.
Bir Bilinmeyenli Denklemler
a, b, c ∈ R olsun,
Bir eşitliğin her iki yanına aynı sayı eklenip çıkarılabilir. Bu durumda eşitlik değişmez.
a = b ise a+c = b+c ve a – c = b – c olur.
Bir eşitliğin her iki yanı sıfırdan farklı bir sayı ile çarpılabilir. Bu durumda eşitlik değişmez.
a=b ise a.c = b.c olur.
a ve b gerçek sayı ve a sıfırdan farklı olmak üzere ax+b=0 ifadesine birinci dereceden bir bilinmeyenli denklem denir. Denklemi sağlayan x değerine denklemin kökü ve ve bu değerlerin oluşturduğu kümeye de denklemin çözüm kümesi denir.
x – 2 = 3 denklemini sağlayan tek bir x değeri vardır ve bu değer 5’tür.
Çözüm
x = 3 + 2
x = 5
Denklemin kökü: 5
Çözüm kümesi: Ç = { 5 }
Denklemler Çözülürken İzlenecek Yollar

Denklem Çözümleri
Örnek
3x − 5 = x + 5 denklemini çözelim.
Bilinmeyenleri eşitliğin bir tarafına, diğer sayıları diğer tarafa toplarız.
3x − x = 5 + 5 (−5 sağa +3 olarak geçer, x sola −x olarak geçer.)
2x = 10 (x’in başındaki 2 katsayısını karşıya bölü olarak geçer.)
x = ![]()
x = 5
Örnek
2(3x − 5) = 8 − 3(x + 4) denklemini çözelim.
6x − 10 = 8 − 3x − 12 (Parantez önlerindeki 2 ve −3 parantezlere dağıtılır.)
6x + 3x = 8 − 12 + 10 (−3x sola +3x olarak, −10 sağa +10 olarak geçer.)
9x = 6 (x’in başındaki 9 katsayısını karşıya bölü olarak geçer.)
x = ![]()
Koordinat Sistemi
İki sayı doğrusunun 0 (sıfır) noktasında birbiriyle dik kesişmesiyle oluşan sisteme kartezyen koordinat sistemi denir. Burada iki sayı doğrusu yani iki boyut olduğu için iki boyutlu kartezyen koordinat sistemi de denir.
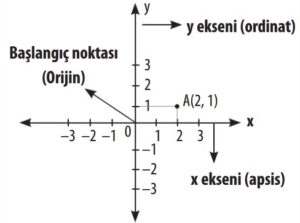
Koordinat sisteminde yatay eksen x ekseni, dikey eksen y ekseni olarak isimlendirilir. x ve y eksenlerinin kesişim noktası başlangıç noktasıdır. Başlangıç noktası orijin olarak isimlendirilir.
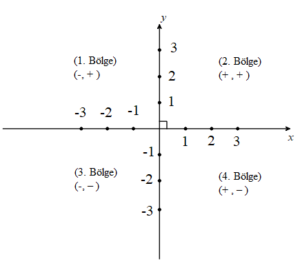
Koordinat sistemini oluşturan ve dik kesişen x ve y eksenleri analitik düzlem üzerinde 4 bölge meydana getirirler. Bu bölgeler saat yönünün tersine doğru 1. bölge, 2. bölge, 3. bölge ve 4. bölge olarak adlandırılırlar.
Şekilde de verildiği gibi bileşenleri A(x, y) olan bir nokta,
*x ve y pozitif ise 1. bölgede,
*x negatif ve y pozitif ise 2. bölgede,
*x ve y her ikisi de negatif ise 3. bölge,
*x pozitif ve y negatif ise 4. bölgededir.
Örnek:
Koordinat sisteminde A(2,-5) noktasının x eksenine olan uzaklığı kaç birimdir?
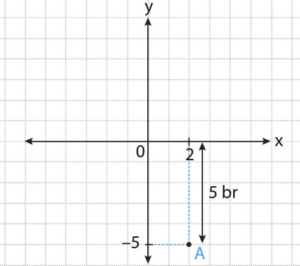
Doğrusal İlişki ve Doğrusal Denklemler
Doğrusal İlişki Nedir?
İki değişken arasındaki ilişkinin grafiği doğru şeklinde ise bu iki değişken arasında doğrusal ilişki vardır deriz.
Değişkenlerden değeri başka bir değişkene bağlı olarak değişen değişkene bağımlı değişken, değerini kendi belirlediğimiz değişkene bağımsız değişken denir.
Doğrusal Denklemler Nedir?
Doğrusal ilişkiyi ifade eden denklemlere doğrusal denklem denir. x ve y değişken, a ve b katsayı ve c sabit terim olmak üzere: ax + by + c = 0 biçiminde olan denklemlere doğrusal denklem denir. Doğrusal denklemde a ve b katsayılarının ikisi birden 0 olamaz. Yani denklemde en az bir tane bilinmeyen bulunmalıdır.
Örnek:
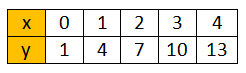
Tablodaki x ve y arasındaki ilişkiler nelerdir?
y değişkeni üçer arttığı için → y=3x
x=0 iken y=1 ise
Bu yüzden y=3x+1 olmalıdır.
Doğrusal Denklemlerin Grafikleri
1. Eğimi ve Bir Noktası Bilinen Doğru Denklemi

2. İki Noktası Bilinen Doğrunun Denklemi
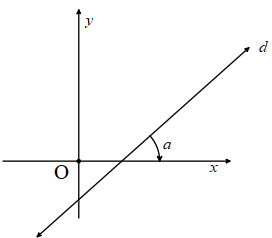
İki noktası bilinen doğrunun denklemini yazmak için;
İki noktadan geçen doğrunun eğimi bulunur.
Bulunan eğim ve verilen noktalardan herhangi biri kullanılarak doğru denklemi yazılır.
3. Eksenleri Kestiği Noktaları Bilinen Doğrunun Denklemi
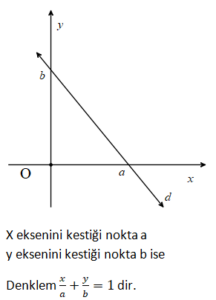
4. Eksenlere Paralel Doğruların Denklemi
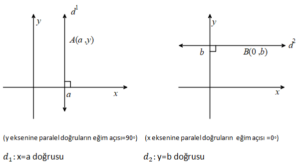
5. Orjinden Geçen Doğru Denklemi
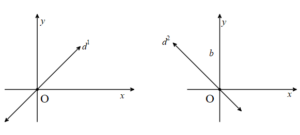
Orjin noktası olan O(0,0)’dan geçen ve eğimi m olan doğru denklemi
y-0=m(x-0)
y=mx’dir
Denklemi Verilen Doğrunun Grafiği

Eğim
Bir dik üçgende dikey uzunluğun, yatay uzunluğa oranına eğim denir. Eğim “m” harfi ile gösterilir.
![]()
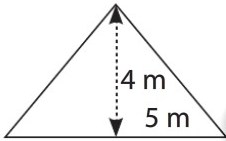
Üçgenin eğimini bulalım

Doğrunun Eğimi
Bir doğrunun eğimi, doğru üzerinde bulunan iki nokta arasındaki dikey değişimin yatay değişime oranıdır. y eksenine göre sağa yatık doğruların eğimi pozitif, sola yatık doğruların eğimi negatiftir.
Örnek:
Orjinden ve A(3,6) noktasından geçen doğrunun denklemini yazalım.
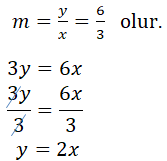







Gerçekten çok yararlı ve tam gereğinde bir konu anlatımı olmuş proje ödevime çok yardımcı oldunuz çok teşekkürler kısa ve öz yazıları ile bende bu projeden 100 alacağım :)))
Mat ödev vardı derman gibi geldi
Evet site muq olmuş ya
Yapanın ellerine sağlık 😊
O kada teşekkür ederim ki özet ödevim vardı çok yararlı oldu
Çok güzel olmuş ben çok beğendim
Güzel gibi görünüyor.Umarım anlarım.
Güzel bir siteye genziyor
Çok güzel bir naltımdı teşekkür ediyorum. 🤗🤍💜💜💜
Bencede baya iyi naltım
Bende beğendim