Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak  bilgi sahibi olabilirsiniz. Fonksiyonlar konusu ile ilgili bütün soruların cevabı sizleri bekliyor…

Fonksiyonlar

• Fonksiyon Kavramı ve Gösterimi
  • Fonksiyon Kavramı
  • Fonksiyon Türleri
  • Fonksiyonlarda Dört İşlem
  • Fonksiyonların Grafikleri
•  İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi
  • Fonksiyonlarda Bileşke İşlemi
  • Fonksiyonun Tersi

Fonksiyon Kavramı ve Gösterimi

Fonksiyon Kavramı

Boş kümeden farklı A ve B kümeleri için A nın her bir elemanını B nin bir tek elemanı ile eşleyen kurala A dan B ye fonksiyon denir ve genellikle f, g, h, veya F, G, H, sembolleriyle gösterilir.

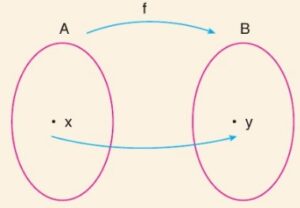
Yukarıda Venn şemasıyla gösterimde x ∈ A elemanın, y ∈ B elemanına eşleyen kural f ile gösterilmiştir. Bunu

f: A → B biçiminde ifade ederiz ve B deki y elemanı A daki x elemanına f kuralı ile bağlıdır deriz. Yani
f: A → B
x → y

x in f kuralı altındaki görüntüsü y dir denir.

Bunu f(x) = y şeklinde de gösteririz.

f: A → B gösteriminde A ya fonksiyonun tanım kümesi B ye fonksiyonun değer kümesi denir. Tanım kümesinin f kuralı altındaki görüntülerinin oluşturduğu f(A) kümesine de görüntü kümesi denir.

Fonksiyon Türleri

Bire-bir Fonksiyon:  Tanım kümesindeki farklı kişilerin yaşları da farklı olduğu görülmektedir.

Genel olarak f: A → B, y = f(x) fonksiyonu verilsin. A tanım kümesindeki farklı iki elemanın eğer görüntüleri de farklı oluyorsa f ye bire bir fonksiyon denir. Yani her x₁, x₂ ∈ A için eğer x₁ ≠ x₂ iken f(x₁) ≠ f(x₂) oluyorsa f ye bire bir (1 – 1) fonksiyon denir.

Örten Fonksiyon:  Değer kümesinde boşta eleman kalmıyorsa fonksiyon örten ‘dir. Başka bir deyişle, görüntü kümesi değer kümesine eşit olan fonksiyonlar örtendir.

İçine Fonksiyon: Örten olmayan fonksiyona içine fonksiyon denir.

Bazı Özel Fonksiyonlar: Sabit, Doğrusal, Birim, Parçalı, Permütasyon

Sabit Fonksiyon: Tanım kümesindeki her eleman değer kümesinde yalnızca bir elemanla eşleşen fonksiyonlara sabit fonksiyon denir. c bir gerçek sayı olmak üzere sabit fonksiyonlar f(x) = c biçiminde gösterilir.

Hatırlatma:  y = f(x) = c sabit fonksiyonunda x li terimler olmaz.

Birim Fonksiyon:  Tanım kümesindeki her elemanı yine kendisine dönüştüren kurala birim fonksiyon denir ve f(x) = x biçiminde gösterilir.

f: R → R, f(x) = x in grafiği çizilirken y = x doğusunu çizmek yeterlidir.

Hatırlatma: y = f(x) = x fonksiyonuna I. açıortay doğrusu denir. f(x) = x birim fonksiyonunda x li terim dışında hiçbir terim olmamalıdır.

Parçalı Fonksiyon:

Tanım kümesini parçalara ayırıp bunların her biri için farklı kurallar içeren fonksiyon parçalı bir fonksiyondur.

x<o ise görüntüsünü bulmak için 2x+1 değilse 3x-4’ü kullanmalıyız.

Permütasyon fonksiyon: Bir kümeden kendisine yazılan bire-bir ve örten fonksiyonlara permütasyon denir.

f: A → A

f = fonksiyonu permütasyon fonksiyon olup;

Doğrusal Fonksiyon: f(x)=ax+b| şeklindeki fonksiyonlar doğrusaldır. Grafikleri kartezyen düzlemde bir doğru oluşturur. Doğrusal fonksiyonlar, bire-birlik özelliği incelenirken bir örneğini gördüğümüz gibi, a≠0| ise bire-birdir. Doğrunun ayırıcı özelliği eğim dir. Eğim, x| teki 1 br lik artışın y| de yarattığı değişimdir.

Fonksiyonlarda Dört İşlem

Fonksiyonların Grafikleri

f(x) = ax + b fonksiyonunun (Doğrusal fonksiyon) grafiği çizilirken x = 0 için y eksenini kestiği nokta, y = 0 için x eksenini kestiği nokta bulunur. Bu iki noktadan geçen bir doğru çizildiğinde grafik tamamlanır.

 İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi

Fonksiyonlarda Bileşke İşlemi

f: A → B ve g: B → C

fonksiyonları için A kümesindeki her elemanı, C kümesindeki yalnız bir elemana eşleyen fonksiyona bileşke fonksiyon denir. Bu fonksiyon gof şeklinde gösterilir.

gof : A→C

x →(gof) (x) olur.

Bir Fonksiyonun Tersi

10. Sınıf Matematik Konuları için Tıklayınız

10. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız