Denklem Çözme Konu Anlatımı

Matematik ayt konu anlatımı, Matematik tyt konu anlatımı , Matematik yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Denklem Çözme Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.
Denklem Çözme
Birinci Dereceden Bir Bilinmeyenli Denklemler
Kavramlar
a, b, c ∈ R olsun,
Bir eşitliğin her iki yanına aynı sayı eklenip çıkarılabilir. Bu durumda eşitlik değişmez.
a = b ise a+c = b+c ve a – c = b – c olur.
Bir eşitliğin her iki yanı sıfırdan farklı bir sayı ile çarpılabilir. Bu durumda eşitlik değişmez.
a=b ise a.c = b.c olur.
a ve b gerçek sayı ve a sıfırdan farklı olmak üzere ax+b=0 ifadesine birinci dereceden bir bilinmeyenli denklem denir. Denklemi sağlayan x değerine denklemin kökü ve ve bu değerlerin oluşturduğu kümeye de denklemin çözüm kümesi denir.
x – 2 = 3 denklemini sağlayan tek bir x değeri vardır ve bu değer 5’tür.
Çözüm
x = 3 + 2
x = 5
Denklemin kökü: 5
Çözüm kümesi: Ç = { 5 }
Denklemler Çözülürken İzlenecek Yollar

Denklem Çözümleri
Örnek
3x − 5 = x + 5 denklemini çözelim.
Bilinmeyenleri eşitliğin bir tarafına, diğer sayıları diğer tarafa toplarız.
3x − x = 5 + 5 (−5 sağa +5 olarak geçer, x sola −x olarak geçer.)
2x = 10 (x’in başındaki 2 katsayısını karşıya bölü olarak geçer.)
x = ![]()
x = 5
Örnek
2(3x − 5) = 8 − 3(x + 4) denklemini çözelim.
6x − 10 = 8 − 3x − 12 (Parantez önlerindeki 2 ve −3 parantezlere dağıtılır.)
6x + 3x = 8 − 12 + 10 (−3x sola +3x olarak, −10 sağa +10 olarak geçer.)
9x = 6 (x’in başındaki 9 katsayısını karşıya bölü olarak geçer.)
x = ![]()
Birinci Dereceden İki Bilinmeyenli Denklemler
Kavramlar
a, b ve c sabit gerçek sayılar, a ve b sıfırdan farklı olmak üzere, x ve y değişkenleri için ax + by = c şeklinde yazılan ifadelere birinci dereceden iki bilinmeyenli denklem denir.
Değişkenleri birinci dereceden ve aynı olan birden fazla denklem grubuna ise birinci dereceden iki bilinmeyenli denklem sistemi denir. Bir denklem sisteminin çözüm kümesi, bu iki denklemi aynı anda sağlayan (x, y) sıralı ikilileridir.
Birinci Dereceden İki Bilinmeyenli Denklemlerin Grafikleri
Birinci dereceden iki bilinmeyenli denklemlerin grafikleri koordinat sisteminde bir doğru belirtir. Bu doğru, denklemi sağlayan (x, y) sıralı ikililerinin temsil ettiği noktalardan geçer.
Örnek
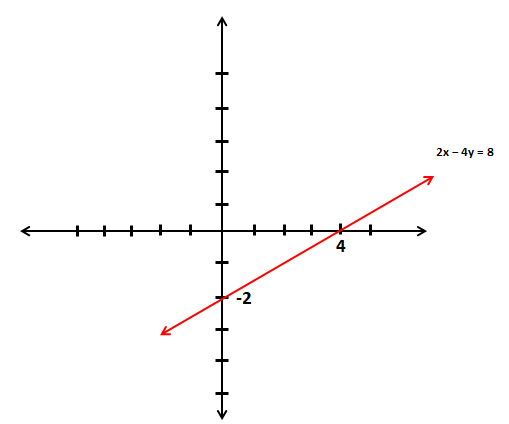
2x − 4y = 8 denkleminin grafiğini çizelim.
Doğrunun eksenleri kestiği noktaları buluruz. Bu noktaları koordinat sisteminde işaretleyerek grafiği çizeriz.
| x | y | (x , y) |
| 0 | −2 | (0 , −2) |
| 4 | 0 | (4 , 0) |
Örnek
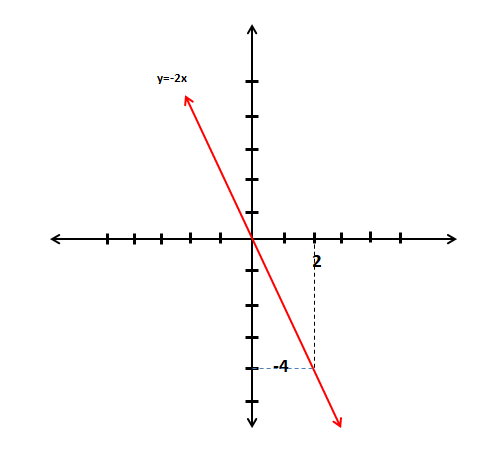
y = −2x denkleminin grafiğini çizelim.
Bu doğru orijinden geçer. Geçtiği ikinci noktayı isteğimize göre belirleyebiliriz. Bu noktaları koordinat sisteminde işaretleyerek grafiği çizeriz.
| x | y | (x , y) |
| 0 | 0 | (0 , 0) |
| 2 | −4 | (2 , −4) |
Denklem Sistemi Çözümü
Bir denklem sisteminin çözüm kümesini sıralı ikilileri tek tek yerine koyarak belirlemek her zaman mümkün olmayabilir. Denklem sistemlerinin çözümlerini bulmak için yerine koyma, yok etme, grafik çizme gibi matematiksel yöntemler kullanılır.
Yerine Koyma Yöntemi
ax + by = c
dx + ey = f
denklem sisteminin yerine koyma yöntemi ile çözümünde; birinci ya da ikinci denklemde x ya da y değişkeni yalnız bırakılarak, elde edilen ifade diğer denklemde yerine yazılır.
Yerine Koyma Yöntemiyle denklem sistemini çözerken genellikle katsayısı 1 olan değişken diğer değişken türünden ifade edilir.
Yok Etme Yöntemi
ax + by = c
dx + ey = f
denklem sisteminin yok etme yönteminde her iki denklem taraf tarafa toplanarak bilinmeyenlerden birisi yok edilir. Verilen denklem sisteminde taraf tarafa toplama işlemi ile bilinmeyenlerden birisi yok olmuyorsa, çarpma işlemi ile bilinmeyenlerden birisinin katsayıları eşit ve zıt işaretli olacak şekilde düzenlenir.
Çözüm Kümesi – Katsayı İlişkisi







