Çember ve Daire Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Çember ve Daire konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Çember ve Daire
- Çemberin Elemanları
- Çemberde Açı Çevrel Çember ve Sinüs Teoremi
- Çemberde Teğet
- Dairenin Çevresi ve Alanı
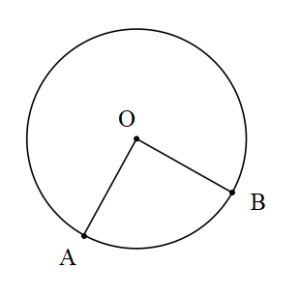
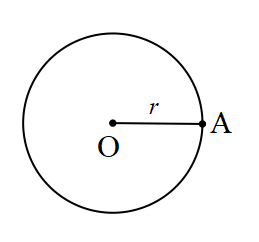
Düzlemde sabit olan bir noktadan eşit uzunluktaki noktaların oluşturduğu kümeye çember denir.
O noktası çemberin merkezi olmak üzere ;
yarıçap=r=|QA|=|OB|
çemberin çapı=|AB|
|AB| =2r’dir.
Çemberin Elemanları
Düzlemde sabit bir noktaya (merkez) eşit uzaklıkta (yarıçap) bulunan noktalar kümesine çember denir.
Yay: Bir çember üzerindeki farklı iki nokta arasında kalan çembere ait noktalar kümesine çember yayı denir.
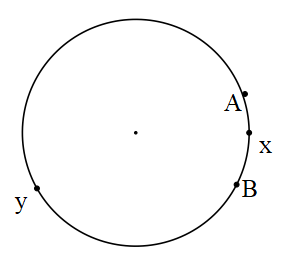
A ve B noktaları arasındaki yaylar AxB ve AyB yaylarıdır.
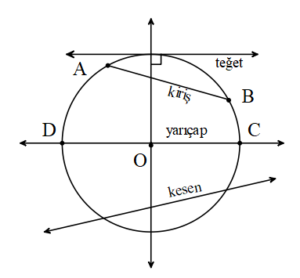
Teğet: Bir çember ile tek bir ortak noktası olan doğruya çemberin bir teğet doğrusu denir.
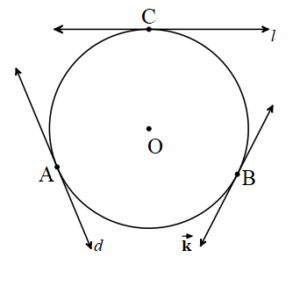
d,k,l O merkezli çemberin herhangi üç teğet doğrusudur.
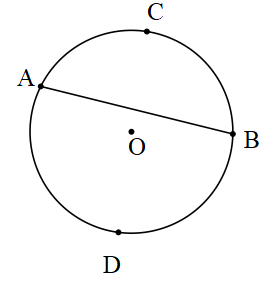
Kesen: Çemberi farklı iki noktada kesen doğruya çemberin keseni denir.
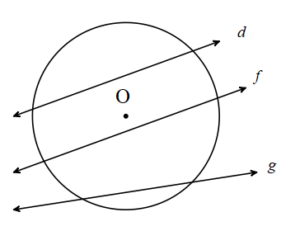
d,e,f doğruları O merkezli çemberin kesenleridir.
Kiriş: Bir çemberin farklı iki noktasını birleştiren doğru parçasına çemberin kirişi denir.
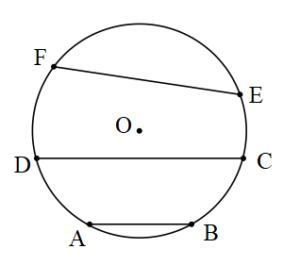
[AB], [DC], [EF] doğru parçaları O merkezli çemberin kirişleridir.
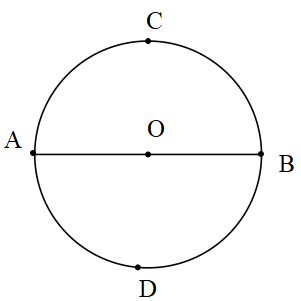
Çap: Merkezden geçen kirişe çap denir.
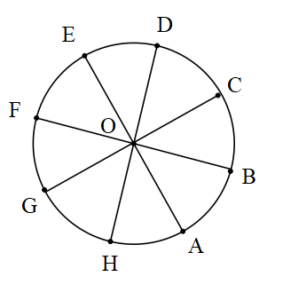
[AE],[BF],[CG],[DH] doğru parçaları O merkezli çemberin çap doğrusudur. Bu doğruların uzunlukları çemberin çap uzunluğu olur.
Bir Düzlemde Bir Çember ile Bir Doğrunun Birbirlerine Göre Durumları
Doğru çemberi kesmez
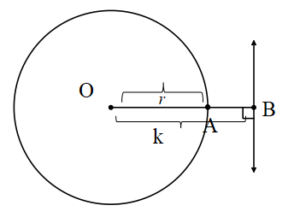
O noktasından doğruya olan uzaklık (dik) yarıçaptan büyük ise doğru ile çember kesişmez.
[OB] ⊥ d, |OA|=r, |OB|=k
k>r ise d∩ Ç= {} olur.
2. Doğru çembere teğet olur.
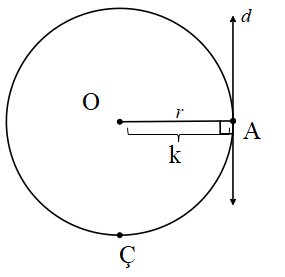
Çemberin merkezinin d doğrusuna olan uzaklığı yarıçapa eşit olduğunda “çeber doğruya teğettir” denir. Çember ile doğrunun bu durumda tek bit ortak noktası (A) olur.
[OA] ⊥ d, |OA|=k
k=r ise d∩ Ç= {A} olur.
3.Çember ile doğru farklı iki noktada kesişir.
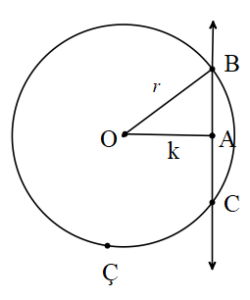
Çember merkezinden doğruya olan uzaklık çemberin yarıçapından küçük ise doğru çemberi iki farklı noktada keser.
[OA] ⊥ d, |OA|=k |OB|=k
r>k ise d∩ Ç= {B,C} dir.
Çemberde Kirişin Özellikleri
1. Bir çemberin merkezinden herhangi bir kirişe çizilen dik doğru kirişi iki eş parçaya ayırır.
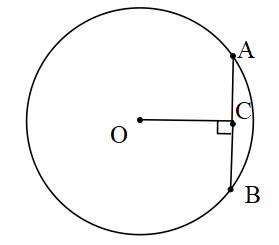
[OC] ⊥ [AB] ⇔ |AC|=|CB|
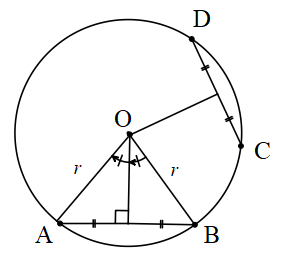
bu durumda AOB üçgeni ikizkenar üçgen olur.
2. Bir çemberde eşit uzunluktaki kirişlerin çemberin merkezine olan uzaklıkları eşittir.
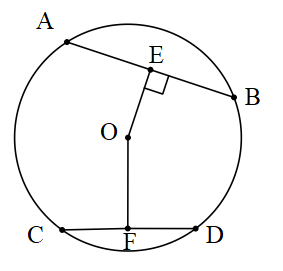
|AB|=|CD| ⇔ |OE|=|OF|
3. Bir çemberde kiriş merkeze yaklaştıkça uzunluğu artar.
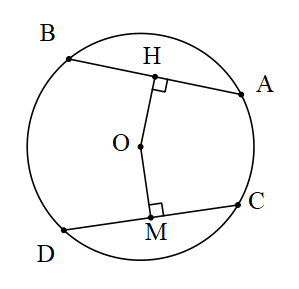
|OH|>|OM| ⇔ |AB|=|CD|
Çemberde Açı Çevrel Çember ve Sinüs Teoremi
Çemberin iki noktası arasında kalan çember parçasına yay denir.


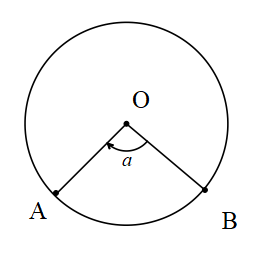
Merkez Açı
O merkez [OA ve [OB ışın AOB açısının gördüğü yay AB yayıdır.
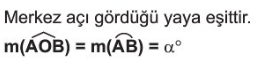
Çevre Açı
Köşesi çember üzerinde ve kenarları çember kirişi olan açıya çevre açı denir.
O merkez [AB] ve [BC] çember krişi B oktası çember üzerinde ve ABC açısının köşesidir.
Çevre açı gördüğü yayın ölçüsünün yarısına eşittir.
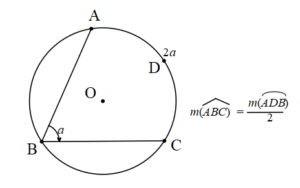
Teğet-Kiriş Açı
Bir çemberde teğet doğrusu ile kiriş arasında kalan açıya teğet kiriş açı denir. A noktası çember ile doğrunun ortak teğet noktasıdır.

Çemberde İç Açı
[BD] ∩[AC]={K} çemberde kesişen iki kirişin oluşturduğu açıya iç açı denir.
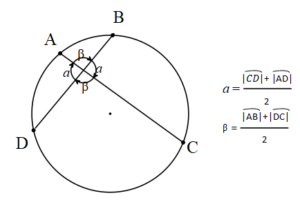
Çemberde Dış Açı
Köşesi (a) çemberin dış bölgesinde olan iki kesenin iki teğetin veya bir teğet ile bir kesenin oluşturduğu açıya dış açı denir.
a,β,θ birer dış açıdır.
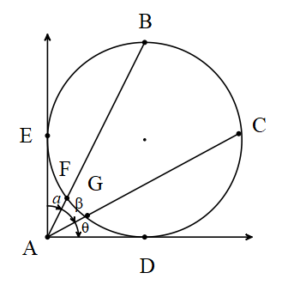
Çemberde dış açı gördüğü çember yayların farkının yarısıdır.
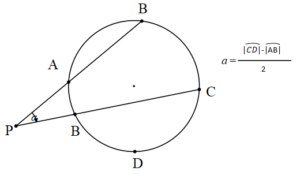
Teğetler Arasında Kalan Dış Açı
A ve B teğet noktalarıdır. APB açısı teğetler arasında kalan açıdır. Bu açı aynı zamanda bir dış açıdır.
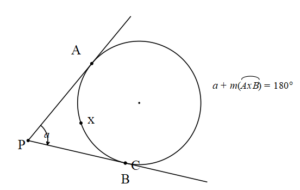
Teğetler arasında açı ile bu açının gördüğü küçük yayın toplamı 180º’dir.
Bir Üçgenin Çevrel Çemberi
O merkezli r yarıçaplı çember ABC üçgeninin çevresel çemberidir.
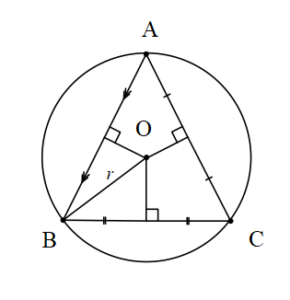
Sinüs Teoremi
Bir ABC üçgeninin çevrel çemberinin yarıçapı r olmak üzere;
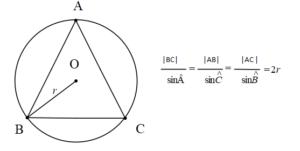
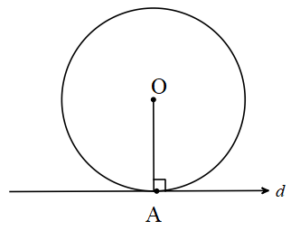
Çemberde Teğet
Bir çembere herhangi bir noktadan çizilen teğet değme noktası olan A’da yarıçapa diktir.
[OA] ⊥ d
1. Bir çembere dışındaki bir noktadan çizilen teğet uzunlukları eşittir.
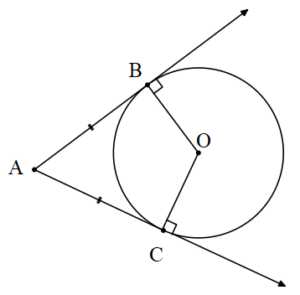
Bir çembere dışındaki bir noktadan çizilen teğetlerin arasında kalan ve çemberi gören açının açıortayı çemberin merkezinden geçer.
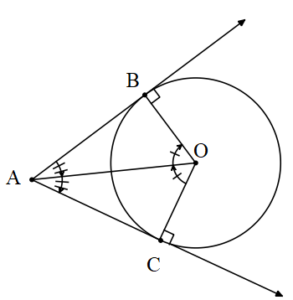
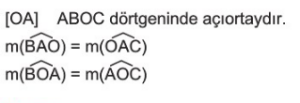
2. İç Teğet Çember
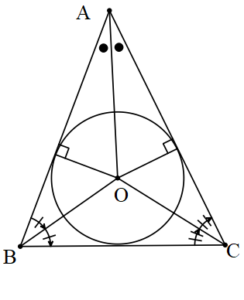
ABC üçgeninde açıortayların kesim noktası iç teğet çemberin merkezi olur.
3. Dış Teğet Çember
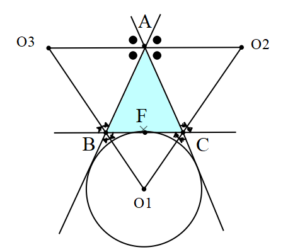
İki dış açının açıortaylarının kesim noktası üçgenin dış teğet çemberinin merkezidir. Şekilde O1, O2, O3 noktaları ABC Üçgeninin dış teğet çemberlerinin merkezleridir.
Dairenin Çevresi ve Alanı
Dairenin Çevresi
O merkezli çemberin yarıçapı r ise
Çevre=2.π.r‘dir

Daire Dilimin Yay Uzunluğu
Yarıçapı r olan bir çemberde a derecelik merkez açının gördüğü AxB yayının uzunluğu;
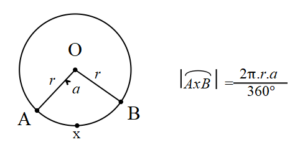
şeklinde hesaplanır.
Daire ve Alanı
Çember ve iç bölge birleşimine daire denir.
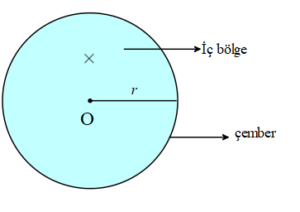
Dairenin Alanı =π.r2 birimkaredir.
Daire Diliminin Alanı
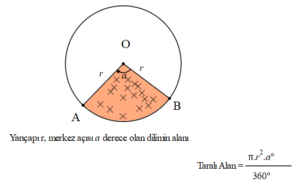







Emeği olan herkese teşekkür ederiz.
Çok teşekkür ederim bana faydası bayağı oldu.Allah sizden razı olsun inşallah 🙏❤️🥰
Çok teşekkür ederim Allah sizden razı olsun.❤️❤️🥰🥰
Güzel tekrar oldu mat sınavında zortlamayalım
teşekkür ederim
Ben Bunları Ezberleyebiliyorsam Okulda İşim Ne ??
BOŞYAPCAKSAN BURDA NE İŞİN VAR KARDEİ
Ali biçim abi gerçekten sen misin
Hulk abi gerçekten sen misin
Eren gerçekten sen misin?
Elif gerçekten sen misin?
birisi gerçekten sen misin ?
Mikasa Gerçekten Sen Misin?
furkan gerçekten sen misin?
akıl sağlığımı kaybettim?
Akıl sağlığım gerçekten sen misin?
Sütlü makarna gerçekten sen misin?
Mehmet, gerçekten sen misin?
evet benim
Evet gerçekten sen misin?
evet benim gerçekten sen misin
İşte ezberleyenediğin için okuldasın
Nuri gerçekten sen misin
Adem gerçekten sen misin?
kulanıcı gerçekten sen misin
Merve gerçekten sen misin?
Cansel gerçekten sen misin
Mehmet gerçekten sen misin
ahmet gercekten sen misin?
canan gercekten sen misin?
ÇOK HARİKA OLMUŞ