7. Sınıf Rasyonel Sayılarla İşlemler Konu Anlatımı
Paydası sıfır olmamak şartıyla, iki tam sayının birbirine oranı şeklinde yazılabilen sayılara rasyonel sayılar denir. 7. Sınıf Rasyonel Sayılar Konu Anlatımı, 7. Sınıf Rasyonel Sayılar , Rasyonel Sayılar Konu Anlatımı, 7. Sınıf Matematik, 7. Sınıf Matematik Konu Anlatımı, Rasyonel Sayılar
Rasyonel Sayılarla İşlemler
- Rasyonel Sayılarla Toplama ve Çıkarma İşlemleri
- Rasyonel Sayılarla Çarpma ve Bölme İşlemleri
- Rasyonel Sayıların Karesinin ve Küplerinin Hesaplanması
- Rasyonel Sayılarla Çok Adımlı İşlemler
- Rasyonel Sayılarla İşlem Yapmayı Gerektiren Problemler
Rasyonel Sayılarla Toplama ve Çıkarma İşlemleri
Rasyonel Sayılarda Toplama İşlemi
Rasyonel sayılarla toplama işlemi yapılabilmesi için işlemdeki rasyonel sayıların paydaları eşit olmalıdır.
Aynı işaretli rasyonel sayılar toplanırken paydalar eşit değilse önce paydalar eşitlenir. Daha sonra payların mutlak değerleri toplanıp toplamın payı olarak, ortak payda ise toplamın paydası olarak yazılır. Rasyonel sayıların ortak işareti toplamın işareti olur.
•Paydalar eşit ise paylar toplamı bulunur ve ortak payda aynen yazılır.
Örnek:
işleminin sonucu kaçtır?
Çözüm:
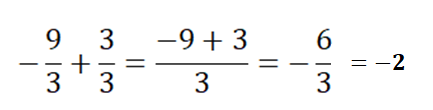
• Paydaları eşit olmayan rasyonel sayılarla toplama işlemi yapılırken paydalar eşitlenir, paylar toplanır ve ortak
payda aynen yazılır.
Örnek:
işleminin sonucu kaçtır?
Çözüm:
Paydaları eşitleyerek işleme başlayalım.
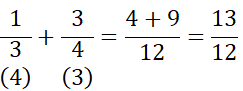
Rasyonel Sayılarda Çıkarma İşlemi
Rasyonel sayılarla çıkarma işlemi yapılırken sayıların paydalarına bakılır:
• Paydalar eşit ise paylar farkı bulunur ve ortak payda aynen yazılır.
Örnek
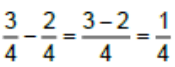
• Paydaları eşit olmayan rasyonel sayılarla çıkarma işlemi yapılırken paydalar eşitlenir, paylar arasındaki fark bulunur ve ortak payda aynen yazılır.
Örnek
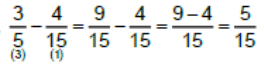
Rasyonel Sayılarla Çarpma ve Bölme İşlemleri
Rasyonel Sayılarla Çarpma İşlemi
Rasyonel sayılarla çarpma işleminde payların çarpımı, çarpımın payına paydaların çarpımı ise çarpımın paydasına yazılır.
Çarpılan sayılarda tam sayılı kesir varsa bileşik kesre çevrilir.
Çarpılan sayılarda tam sayı varsa paydasına 1 yazılır.
Varsa sadeleştirme yapılır. Sadeleştirme yaparken çarpılan sayılarda paydaki herhangi bir sayı ile paydadaki herhangi bir sayı sadeleştirilebilir.
İşlem yapılırken:
Çarpanlardaki paylar çarpılıp sonucun payına, paydalar çarpılıp sonucun paydasına yazılır.
Örnek:
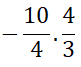
işleminin sonucu kaçtır?
Çözüm:
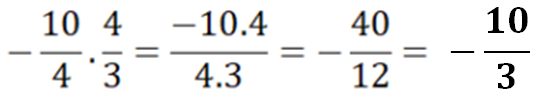
sadeleştirme yapılarak bu sonuca ulaşılır.
Rasyonel Sayılarla Çarpma İşleminin Özellikleri
Rasyonel Sayılarla Bölme İşlemi
İki rasyonel sayıyı birbirine bölme işlemini de, kesirlerle bölme işlemini yaptığımız gibi yaparız.
Örnek:
işlemin sonucu kaçır?
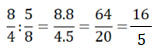
Rasyonel Sayıların Karesinin ve Küplerinin Hesaplanması
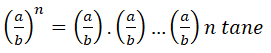
Bir kesrin kuvveti bu kesrinden kaç tanesinin birbiri ile çarpıldığını gösterir.
Örnek
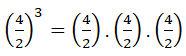
Kesirli sayının kuvveti pay ve paydaya yazılabilir.
Örnek:
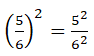
Rasyonel Sayılarla Çok Adımlı İşlemler
Parantez kullanılarak verilen işlemlerde önce parantez içindeki işlemler işlem önceliği dikkate alınarak yapılır. İç
içe parantez varsa önce en içteki parantezden başlamak üzere işlem yapılır.
Örnek
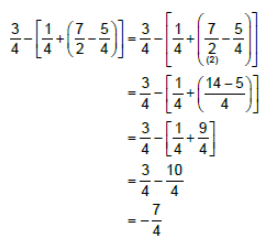
Örnek
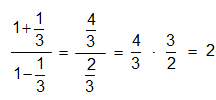
Rasyonel Sayılarla İşlem Yapmayı Gerektiren Problemler
Bir problemi çözerken aşağıdaki adımları mutlaka göz önünde bulundurmalıyız.
1. Problemi Anlama
Problemde bize verilen bilgileri ve bizden istenenleri iyi anlamalıyız.
2. Plan Yapma
Elimizdeki bilgilerle, bizden istenene ulaşmak için nasıl bir yol izlememiz gerektiğini adım adım belirlediğimizde,
problemin çözüm yolunu bulmuş oluruz.
3. Planı Uygulama
Belirlediğimiz adımlar ile ilgili işlemleri yaparken işlem hatası yapmamaya özen göstermeliyiz.
4. Çözümü Kontrol Etme
Problemi bir başka yoldan çözme, geriye doğru işlem yapma gibi birçok farklı şekilde bulduğumuz çözümün, doğruluğunu kontrol edebiliriz. Çözümü kontrol ettiğimizde de aynı sonuca ulaşıyorsak bulduğumuz sonucun doğru olduğunu söyleyebiliriz.
Örnek
Fatma kitabının  
‘ sinin 
‘ni okumuÅŸtur. Fatma 25 sayfa okuduÄŸuna göre kitabın tamamı kaç sayfadır?
 i 25 olan sayıyı bulalım.
25 : 1 = 25
25 . 6 = 150
