7. Sınıf İki Paralel Doğruyla Bir Kesenin Oluşturduğu Açılar Konu Anlatımı

Düzlemde uç noktaları ortak olan iki ışının birleşimine açı denir. Ölçüsü tam olarak 180 derece olan açılara doğru açı denmektedir. 7. Sınıf Doğrular ve Açılar Konu Anlatımı, 7. Sınıf Doğrular ve Açılar , Doğrular ve Açılar Konu Anlatımı, 7. Sınıf Matematik , 7. Sınıf Matematik Konu Anlatımı, Doğrular ve Açılar
İki Paralel Doğruyla Bir Kesenin Oluşturduğu Açılar
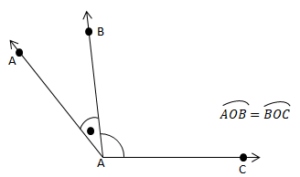
Komşu Açılar
Köşeleri ve birer kenarları ortak olan iki açıya komşu açı denir.
Örnek:
Tümleri ile bütünlerinin ölçüleri toplamının ![]() üne eşit olan açı kaç derecedir?
üne eşit olan açı kaç derecedir?
Çözüm:
Açı: a Tümleri: 90-a Bütünleri: 180-a
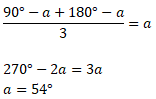
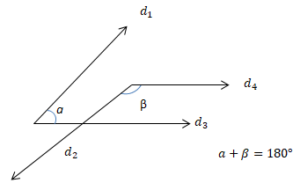
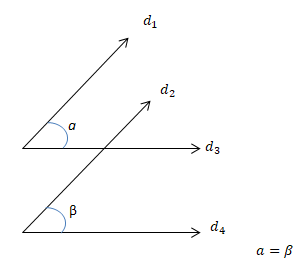
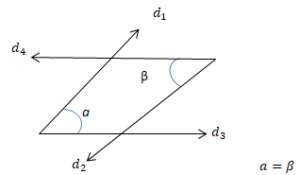
Yöndeş-Ters-İç Ters-Dış Ters Açılar
İki doğrunun bir kesenle oluşturduğu açılardan bu iki doğru arasında kalan açılara iç açılar denir. Kesenin farklı tarafında bulunan ve komşu olmayan iç açılara ise iç ters açılar adı verilir. İki doğrunun bir kesenle oluşturduğu açılardan bu iki doğru arasında olmayan açılara dış açılar denir. Kesenin farklı tarafında bulunan ve komşu olmayan dış açılara ise dış ters açılar adı verilir. İki doğruyu bir kesenle kestiğimizde kesenin aynı tarafında olan biri içte, diğeri dışta kalan açılara yöndeş açılar denir. Doğrular paralel olduğu zaman, iç ters açıların ölçüleri, dış ters açıların ölçüleri ve yöndeş açıların ölçüleri eşit olur.
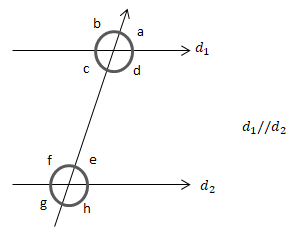
Yöndeş açıların ölçüleri eşittir.
Yöndeş Ters İç Ters Dış Ters
Açılar Açılar Açılar Açılar
a=e a=c c=e a=g
b=f b=d d=f b=h
c=g e=g
d=h f=h
Ters açıların ölçüleri eşittir. İç ters veya dış ters açıların ölçüleri eşittir.
Örnek
x kaçtır?
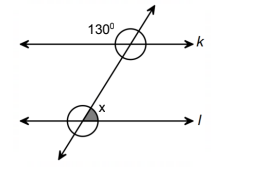
180° – 130° = 50°
Örnek
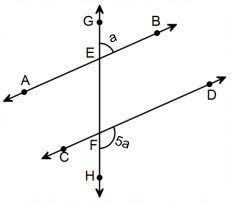
5a + a = 180°
6a = 180°
a = 30°
Karşı Durumlu Açılar
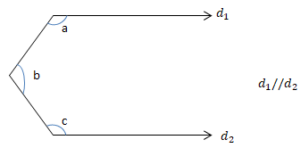
a + c + b= 180°
Örnek
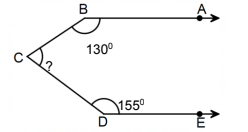
bilinmeyen açıya x diyelim.
130° + 155° + x = 360°
285° + x = 360°
x = 75°
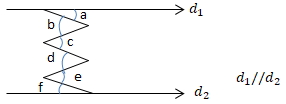
a + c + e = b + d + f
Örnek
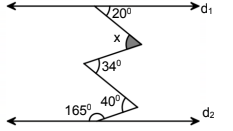
180°- 165° = 15°
15° + 20° +34° = 40° + x
69° = 40° + x
x= 29°
Kenarları Paralel Açılar
![]() olmak üzere,
olmak üzere,