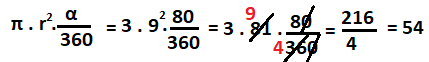7. Sınıf Çember ve Daire Konu Anlatımı

Sabit bir noktaya eşit uzaklıkta noktaların kümesine çember denir. Çember ile çemberin iç bölgesinin birleşimine daire denir. Merkez Açı, Gördüğü Yayın Ölçüsü, Çemberin ve Çember Parçasının Uzunluğunu Bulma, Dairenin ve Daire Diliminin Alanını Bulma 7. Sınıf Çember ve Daire Konu Anlatımı, 7. Sınıf Çember ve Daire , Çember ve Daire Konu Anlatımı, 7. Sınıf Matematik , 7. Sınıf Matematik Konu Anlatımı, Çember ve Daire

Çember ve Daire

• Çemberde Merkez Açı
• Çemberin ve Çember Parçasının Uzunluğu
• Dairenin ve Daire Diliminin Alanı

Çemberde Merkez Açı

Merkez Açı

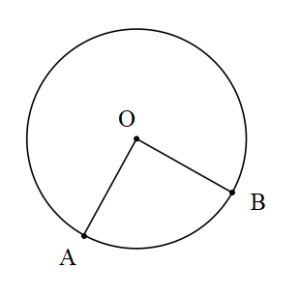
O merkez [OA ve [OB ışın AOB açısının gördüğü yay AB yayıdır.

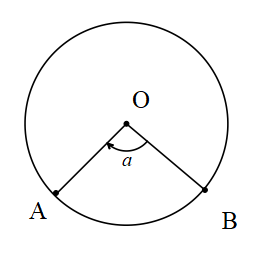
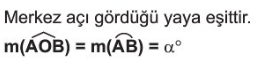
Açıların olduğu gibi yayların da ölçüsü vardır ve dereceyle ölçülür. Çemberin tamamı 360°’dir. Yarım çember yayının ölçüsü 180° , çeyrek çember yayının ölçüsü ise 90°’dir.

Örnek

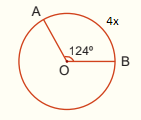
Verilenlere x kaçtır?

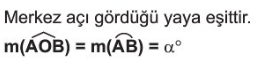olduğuna göre

124 = 4x
x= 124/4
x= 31

Çemberin ve Çember Parçasının Uzunluğu

Çemberin Uzunluğu

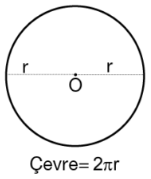
Çemberin yarıçapı r ise çevresinin uzunluğunun 2.π.r formülü ile hesaplanır.

Örnek-1

Yarıçapının uzunluğu 9 cm olan bir çemberin uzunluğunu bulalım. (π = 3 alınız.)

Çemberin çevre uzunluğu = 2.π.r = 2.3.9 = 54 cm’dir.

Örnek-2

Çapının uzunluğu 10 cm olan bir çemberin uzunluğunu bulalım. (π = 3 alınız.)

Önce yarı çapını bulalım.

10:2 = 5

Çemberin çevre uzunluğu = 2.π.r = 2.3.5= 30 cm’dir.

Örnek-3

Yarıçapının uzunluğu 8 cm olan çeyrek çemberin uzunluğunu bulalım. (π = 3 alınız.)

Çemberin çevre uzunluğu = 2.π.r = 2.3.8 = 48 cm’dir.

Soruda bize çeyrek çemberi sorduğu için 4’e böleriz ve 12 cm buluruz.

Çember Parçasının Uzunluğu

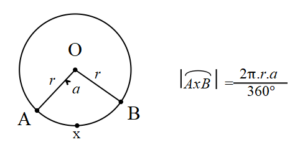
Yarıçapı r olan bir çemberde a derecelik merkez açının gördüğü AxB yayının uzunluğu;

Örnek-1

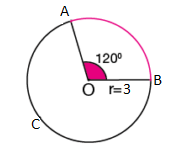
Yukarıdaki verilen çemberde AB yayının uzunluğunu hesaplayınız.

(π=3 alınız)

Dairenin ve Daire Diliminin Alanı

Dairenin Alanı

Daire, çember ile çemberin iç bölgesinin birleşiminden oluşur.

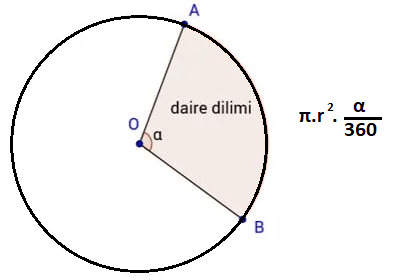
Dairenin yarıçapı r ise alanı π.r2 formülü ile hesaplanır. Daire diliminin alanı ise merkez açısının 360° ile oranıyla dairenin alanının çarpımıyla bulunabilir.

Örnek-1

Yarıçapının uzunluğu 8 cm olan bir dairenin alanını bulalım. (π = 3 alınız.)

Dairenin alanı = π.r^.2 = 3. 8 ² =  = 192 cm²‘dir.

Örnek-2

Yarıçapının uzunluğu 12 cm olan yarım dairenin alanını bulalım. (π = 3 alınız.)

Dairenin alanı = π.r² = 3.12² = 3.144 = 432 cm²‘dir.

Daire Diliminin Alanı

Örnek-1

Yarıçapı 6 cm olan 120 derecelik daire diliminin alanını bulunuz. (π=3 alınız.)

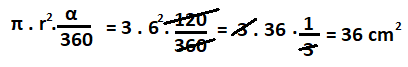
Örnek-2

O merkezli dairenin yarıçapının uzunluğu 9 cm ve merkez açısının ölçüsü 80° olduğuna bilinen daire diliminin alanı kaç cm²‘dir? (π = 3 alınız.)

7. Sınıf Matematik Konuları için tıklayınız.