Türev Konu Anlatımı
Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Türev konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Türev
Türevin Tanımı
Bir fonksiyonun tanımlı olduğu bir noktadaki türevi, fonksiyonun o noktadaki teğet doğrusunun eğimine eşittir.
f:[a,b] -> R bir fonksiyon ve x0(a,b) olsun.
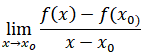limiti bir reel sayı ise, bu limit değerine f fonksiyonunun x0 daki türevi denir.
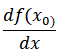ile gösterilir. Buna göre;
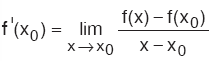dır.
Örnek:
f(x) = |x2 – 16| fonksiyonu için eğer varsa,
a) f'(3) türevini bulalım.
Çözüm:
a) x=3 f(x) = |x2 – 32| fonksiyonu için bir kritik nokta olmadığından
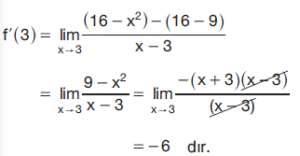
Türev Alma Kuralları
1. xn nin Türevi
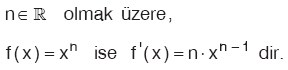
2. c Sabit Sayısının Türevi
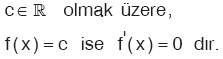
3. c × f(x) in Türevi
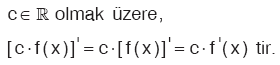
4. Toplamın Türevi
5. Farkın Türevi
6. Çarpımın Türevi
7. Bölümün Türevi
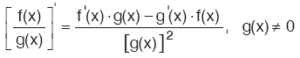
8. Mutlak Değer Fonksiyonunun Türevi
f(a) = 0 ise fonksiyonun bu noktada türevi olabilir ya da olmayabilir. Bunu araştırmak için fonksiyonun sağdan ve soldan türevlerine bakılır. Sağdan ve soldan türevler eşit ise fonksiyon bu noktada türevlidir. Aksi hâlde türevli değildir.
9. İşaret Fonksiyonunun Türevi
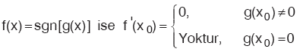
10. Tam Değer Fonksiyonunun Türevi
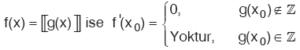
11. Bileşke Fonksiyonun Türevi
f ‘(2) gösterimi [f(2)]’ gösterimi ile karıştırılmamalıdır.f ‘(2) ¹ [f(2)]’ dir. Çünkü f ‘(2) gösterimi, fonksiyonun türevinin, yani f ‘(x) in x = 2 için değeridir.[f(2)]’ gösterimi, fonksiyonun x = 2 için değerinin (Yani, bir reel sayının) türevidir. [f(2)]’ = 0 dır.
Kural:
12. Köklü Fonksiyonun Türevi
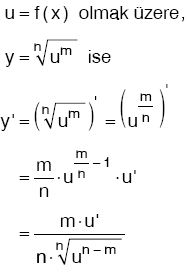
Kural:
13. Logaritmik Fonksiyonun Türevi
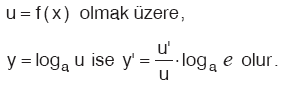
Kural:
14. Üstel Fonksiyonun Türevi
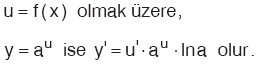
Kural:
15. Parametrik Olarak Verilen Fonksiyonların Türevi
f:A→R fonksiyonu y=f(x) şeklinde belirtileceği gibi g ve h iki fonksiyon olmak üzere;
y=g(t)
x=h(t)
denklemleri ile de belirtilebilir. Burada t ye parametre denir.
Bazen y = g(t) ve x = h(t) denklemlerinden t yok edilerek y = f(x) şeklinde bir denklem elde edilebilir. Ancak bu her zaman mümkün olmayabilir.
Bu durumda,
y = g(t), x = h(t) parametrik denklemleriyle verilen
y = f(x) fonksiyonunun türevi aşağıda verilen kural yardımıyla bulunur.
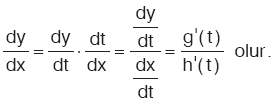
16. Kapalı Fonksiyonların Türevi
F(x, y) = 0 şeklindeki fonksiyonlara kapalı fonksiyon denir.
x in değişken, x in dışında kalanların sabit gibi düşünülmesiyle alınan türevi Fx ile ve y nin değişken, y nin dışında kalanların sabit gibi düşünülmesiyle alınan türevi Fy ile gösterelim.
Buna göre, kapalı fonksiyonun türevini şu kural yardımıyla buluruz:
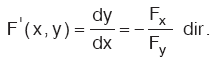
17. Trigonometrik Fonksiyonların Türevi
18. Ardışık Türevler
Kural:
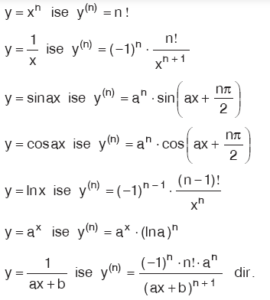
19. Ters Fonksiyonların Türevi
f: A ® B, birebir ve örten bir fonksiyon ise f(x) in tersi olan f–1(x) fonksiyonu bulunur. Sonra türev alınır. Bunun zor olduğu durumlarda ters fonksiyonun türevi şöyle alınır.
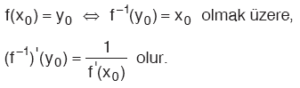
Kural:
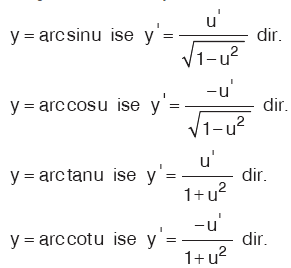
Sağdan ve Soldan Türev
f:[a,b] -> R bir fonksiyon ve x0(a,b) olsun.
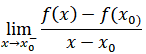Bu limiti varsa bu limite f fonksiyonunun x0 noktasındaki soldan türevi denir.
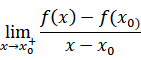Bu limiti varsa bu limite f fonksiyonunun x0 noktasındaki sağdan türevi denir.
f’(x–0) = f’(x+0) = l ise, f fonksiyonunun x=x0 noktasında bir türevi vardır ve f'(x0)=l olur.
f fonksiyonu için f’(x–0) ≠ f’(x+0) ise f fonksiyonunun bu noktada (x0) türevi yoktur.
y =f(x) fonksiyonu (a,b) aralığında türevli ise bu fonksiyonun türev fonksiyonu aşağıdaki şekillerde gösterilir:
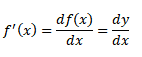
12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.
eyvALLAH