Trigonometri Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Trigonometri konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Trigonometri
Toplam – Fark Formülleri
İki açının toplamının sinüsü, kosinüsü, tanjantı ve kotanjantı

Yarım Açı Formülleri (İki Kat Formülleri)
İki kat açı formülleri ya da Yarım açı formülleri, Trigonometrik değerleri bilinen bir açının iki katının veya yarısının trigonometrik değerlerini hesaplamak için kullanılan formüllerdir. Bu formülleri şöyle sıralayabiliriz:
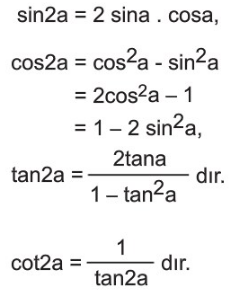
Yarım açı formülleri toplam formüllerinden elde edilen sonuçlardır.

Trigonometrik Denklemler
Sinx=a Denklemi
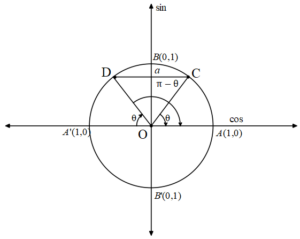
Sinüsü a olan açıların, bitim kenarının birim çemberi kestiği noktalar C ve D dir. Bu nedenle k € Z olmak üzere,
C noktasına, θ+k.2π
D noktasına, π-θ+k.2π gerçek sayıları (açıları) karşılık gelir. Böylece,
sinx=a denkleminin çözüm kümesi,
Ç={x| x=θ + k.2π ∨ x = π-θ + k.2π, k € Z} olur.
cosx=a Denklemi
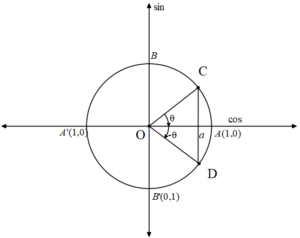
Kosinüsü a olan açıların bitim kenarlrının birim çemberi kestiği noktalar C ve D dir.
C noktasına, θ+k.2π
D noktasına, -θ+k.2π gerçek sayıları (açıları) karşılık gelir. Böylece,
cosx=a denkleminin çözüm kümesi,
Ç={x| x=θ + k.2π ∨ x = -θ + k.2π, k € Z} olur.
tanx =a denklemi
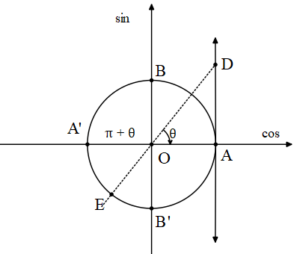
Tanjantı a olan açıların, bitim kenarının tanjant eksenini D noktasında kestiğini görünüz.
θ+kπ açılarının her birinin karşılığı D noktasıdır. Bu nedenle;
tanx= a denkleminin çözüm kümesi
Ç={x| x=θ + k.π ,k € Z} olur.
cotx=a Denklemi
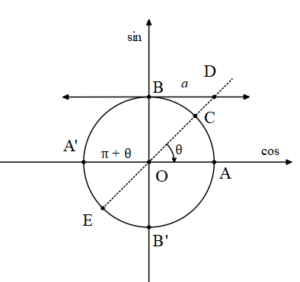
Kotanjantı a olan açıların, bitim kenarının kotanjant eksenini D noktasında kestiğini görürüz.
θ +kπ açılarının her birinin karşılığı D noktasıdır. Bu nedenle;
cotx=a denkleminin çözüm kümesi,
Ç={x| x=θ + k.π ,k € Z} olur.
cosx ve sinx e Göre Lineer Denklemler
a, b, c sıfırdan farklı reel sayılar olmak üzere,
acosx + bsinx = c biçiminde ifade edilen denklemlere, cosx ve sinx e göre, lineer denklemler denir. Bu şekildeki denklemlerin çözülebilmesi için,
a2 + b2 ≥ c2 olmalıdır.
acosx + bsinx = c
denklemi çözülürken, her terim a ya (veya b ye) bölünür.
Denklemde oluşan terimlerden a/b ye (veya b/a ya) tanα denilerek denklem çözülür.
cosx ve sinx e Göre Homojen Denklemler
a ve b sıfırdan farklı reel sayılar olmak üzere,
acosx + bsinx = 0 biçiminde ifade edilen denklemlere homojen denklemler denir. bu denklemler, lineer denklemler gibi çözülebildiği gibi daha kolay yoldan da çözülebilir.
acosx + bsinx = 0 denkleminin her terimi cosx ≠ 0 ile bölünürse,
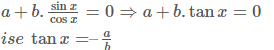 biçiminde elde edilen denklem ile çözülebilir.
biçiminde elde edilen denklem ile çözülebilir.
cosx ve sinx e Göre İkinci Dereceden Homojen Denklemler
a, b, c den en az ikisi sıfırdan farklı reel sayılar olmak üzere;
a.cos2x + b.cosx.sinx + c.sin2x = 0
biçiminde ifade edilen denklemlere ikinci dereceden homojen denklemler denir.
a.cos2x + b.cosx.sinx + c.sin2x = 0 denklemini çözmek için, denklemin her terimi cos2x ≠ 0 ile bölünürse, bu denklem
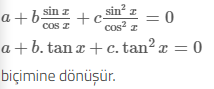
12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.







fazla detay üniversitede görmediğimiz formüller var bukadara gerek yoktu