Geometri ayt konu anlatımı, Geometri tyt konu anlatımı , Geometri yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Özel Üçgenler Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.

Özel Üçgenler

• Kenarlarına Göre Dik Üçgenler
• Açılarına Göre Dik Üçgenler
• İkizkenar Üçgen
• Eşkenar Üçgen

Kenarlarına Göre Dik Üçgenler

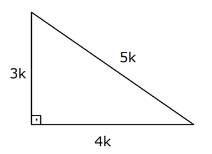
(3 – 4 – 5) Üçgeni

Kenar uzunlukları (3 – 4 – 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir. (6 – 8 – 10), (9 – 12 – 15), … gibi.

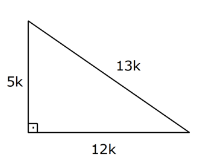
(5 – 12 – 13) Üçgeni

Kenar uzunlukları (5 – 12 – 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir. (10 – 24 – 26), (15 – 36 – 39), … gibi.

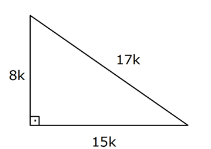
(8 – 15 – 17) Üçgeni

Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir.

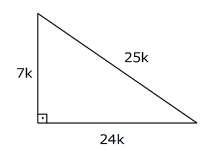
(7 – 24 – 25)Üçgeni

Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir.

Açılarına Göre Dik Üçgenler

30-60-90 Üçgeni

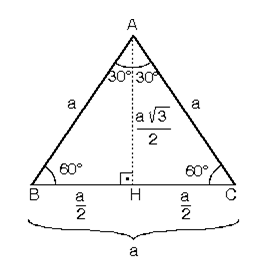
ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° – 60° – 90°) üçgenleri elde edilir.

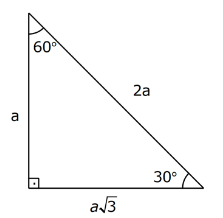
(30° – 60° – 90°) dik üçgeninde; 30°’lik açının karşısındaki kenar hipotenüsün yarısına eşittir. 60°’lik açının karşısındaki kenar, 30° nin karşısındaki kenarın  katıdır.

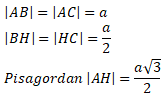
45-45-90 Üçgeni

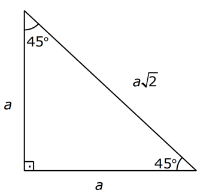
Hipotenüs 45° nin karşısındaki kenarın katıdır.

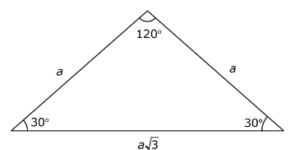
30-30-120 Üçgeni

(30° – 30° – 120°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 120° lik açının karşısındaki kenar olur.

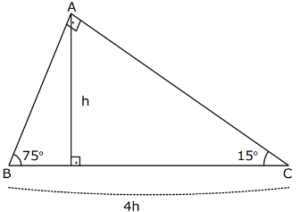
15-75-90 Üçgeni

(15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik |AH| = h dersek, hipotenüs |BC| = 4h olur. Hipotenüs kendisine ait yüksekliğin dört katıdır.

İkizkenar Üçgen

1. İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır.

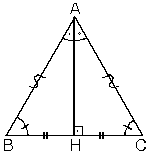
2. Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir.

|AB| = |AC| |BH| = |HC|m(B) = m(C)

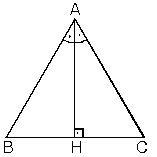
3. Bir üçgende, yükseklik aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.

|AB| = |AC| m(BAH) = m(HAC)m(B) = m(C)

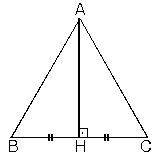
İkizkenar üçgende açıortay, kenarortay ve yüksekliğin aynı olması birçok yerde karşımıza çıktığından çok iyi bilinmesi gereken bir özelliktir.

4. İkizkenar üçgende ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin kesim noktasının ayırdığı parçalarda eşit olur.

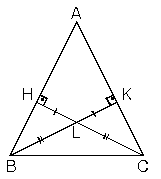
5. İkizkenar üçgende ikizkenara ait kenarortaylar ve kenarortayların kesim noktasının ayırdığı parçalar da birbirine eşittir.

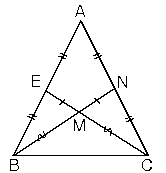
6. İkizkenar üçgende eşit açılara ait açıortaylar da eşittir. Açıortaylar birbirini aynı oranda bölerler.

7. İkizkenar üçgende ikiz olmayan kenar üzerindeki herhangi bir noktadan ikiz kenarlara çizilen dikmelerin toplamı, ikizkenarlara ait yüksekliği verir.

|AB| = |AC| Þ |LC| = |HP| + |KP|

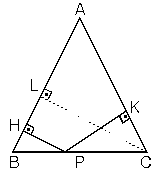
8. İkizkenar üçgende tabandan ikiz kenarlara çizilen paralellerin toplamı, ikiz kenarların uzunluğuna eşittir.

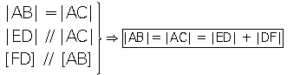
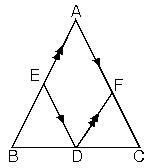
Eşkenar Üçgen

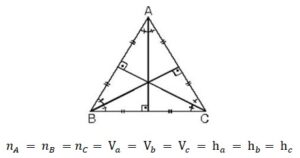
Eşkenar üçgende bütün açıortay, kenarortay yükseklikler çakışık ve hepsinin uzunlukları eşittir.

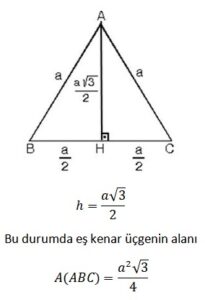
Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı, eşkenar üçgene ait yüksekliği verir. Bir kenarı a olan eşkenar üçgende;

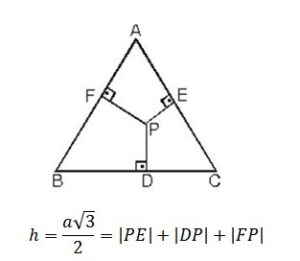
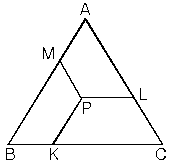
Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen paralellerin toplamı bir kenar uzunluğuna eşittir.

TYT Geometri Konuları Konu Dağılımı için tıklayınız.

AYT Geometri Konuları Konu Dağılımı için tıklayınız.