5. Sınıf Dikdörtgenler Prizmasının Alanı Konu Anlatımı

5. Sınıf Geometrik Cisimler Konu Anlatımı, 5. Sınıf Geometrik Cisimler , Geometrik Cisimler Konu Anlatımı, 5. Sınıf Matematik , 5. Sınıf Matematik Konu Anlatımı, Geometrik Cisimler
Dikdörtgenler Prizmasının Alanı
Dikdörtgenler Prizmasının Alanı
Dikdörtgenler prizmasının alanı bulunurken bütün yüzeylerin alanı toplanarak bulunur. karşılıklı birbirine bakan yüzeylerin alanları eşittir.
Dikdörtgenin alanı = kısa kenar x uzun kenar
Dikdörtgenler Prizmasının Alanı = Ön yüz + Arka yüz + Sağ yüz + Sol yüz+ Üst yüz + Alt yüz
Vereceğimiz örnekle alan nasıl bulunur bulalım.
Örnek
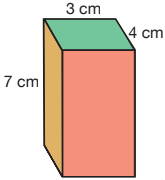
Dikdörtgen prizmanın açınımına bakalım.
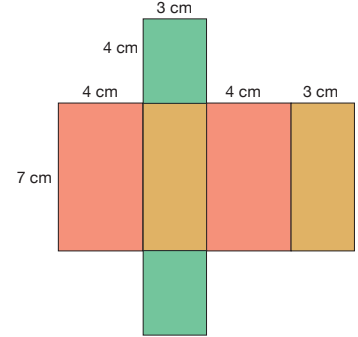
Şekli incelediğimizde her bir dikdörtgenden ikişer tane olduğunu görüyoruz.
7 cm x 4 cm = 28 cm2
2 x 28 cm2 = 56 cm2
7 cm x 3 cm = 21 cm2
2 x 21 cm2 = 42 cm2
4 cm x 3 cm = 12 cm2
2 x 12 cm2= 24 cm2
56 cm2 + 42 cm2 + 24 cm2= 122 cm2
Örnek soru
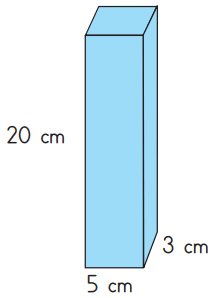
Ayrıt uzunlukları 3 cm, 5 cm ve 20 cm olan dikdörtgen prizmanın ayrıt uzunlukları ikişer cm artırılırsa yüzey alanı kaç cm2 artar?
Dikdörtgenler Prizmasının Alanı = Ön yüz + Arka yüz+ Sağ yüz+ Sol yüz+ Üst yüz + Alt yüz
Dikdörtgenler Prizmasının Alanı = 5 x 20 + 5 x 20 + 3 x 20 + 3 x 20 + 3 x 5 + 3 x 5
Dikdörtgenler Prizmasının Alanı = 100 + 100 + 60 + 60 + 15 + 15 = 350 cm2 artırılmadan olan alanı.
ayrıtları 2 santim artıralım.
Dikdörtgenler Prizmasının Alanı = 7 x 22 + 7 x 22 + 5 x 22 + 5 x 22 + 5 x 7 + 5 x 7
Dikdörtgenler Prizmasının Alanı = 154 +154 + 110 + 110 + 35 + 35 = 598 cm2
598 – 350 =248 cm2 artar.
Kare Prizmanın Alanı
Kare prizmanın yüzey alanı bulunurken tüm yüzlerin alanları bulunur ve toplanır. Kare prizmanın taban alanları birbirine eşit ve yan yüzey alanları birbirine eşittir.
kenar uzunluğuna a dersek
Karenin alanı = a x a
Dikdörtgenin alanı = kısa kenar x uzun kenar
Vereceğimiz örnekle alan nasıl bulunur bulalım.
Örnek
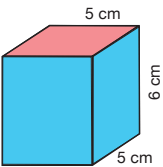
Kare prizmanın açınımına bakalım.
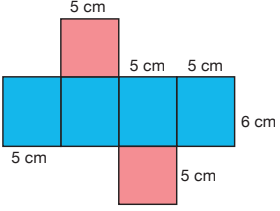
5 cm x 5 cm = 25 cm2
2 x 25 cm2 = 50 cm2
5 cm x 6 cm = 30 cm2
4 x 30 cm2 = 120 cm2
50 cm2 + 120 cm2 = 170 cm2
Küpün Alanı
Küpün yüzey alanı bulunurken tüm yüzlerin alanları bulunur ve toplanır. Küpüm tüm yüzey alanları karedir ve birbirine eşittir.
kenar uzunluğuna a dersek
Karenin alanı = a x a
Vereceğimiz örnekle alan nasıl bulunur bulalım.
Örnek
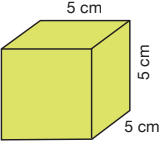
Küpün açınımına bakalım.
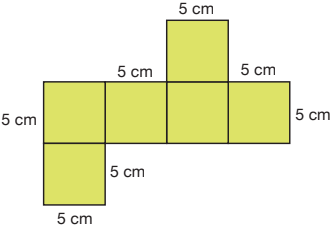
5 cm x 5 cm = 25 cm2
6 x 25 cm2= 150 cm2






